Bubble Sort adalah metode pengurutan data dengan prinsip: data di lokasi/indeks I dibandingkan dengan data lain di lokasi/indeks sebelahnya I+1, apabila terdapat ketidakcocokan data, maka data di lokasi I tersebut akan ditukar dengan data di lokasi I+1. Maka secara perlahan, data akan bergerak menuju ke lokasi yang tepat. Dari sifat inilah, istilah bubble yang artinya gelembung diambil. Seperti gelembung dalam minuman soda, yang perlahan bergerak naik ke atas.
Disajikan contoh cara kerjanya, untuk 5 buah data yaitu 4, 5, 1, 3, 2. Pengurutan dimulai dari lokasi pertama (I adalah 1), dan dibandingkan dengan lokasi sebelahnya (I+1 adalah 2). Karena data 4 dan 5 sudah berada pada urutan yang cocok, maka tidak terjadi pertukaran. Kemudian dicek data lokasi berikutnya (I adalah 2) dengan lokasi sebelahnya (I+1 adalah 3), ternyata data 5 dan 1 tidak cocok, maka ditukar. Lokasi berikutnya (I adalah 3) dibandingkan dengan lokasi sebelahnya (I+1 adalah 4), ternyata data 5 dan 3, tidak cocok lagi, maka ditukar lagi. Demikian seterusnya, dikerjakan sampai dipastikan bahwa semua data ada pada lokasi yang cocok, yang dilakukan dengan cara sudah tidak ada lagi pertukaran yang dilakukan. Berikut adalah proses perubahan data untuk contoh data 4, 5, 1, 3, 2 tersebut:
Perulangan Pertama (First Pass)
- 4 5 1 3 2 (cocok)
- 4 5 1 3 2 (tukar 5 dan 1) 4 1 5 3 2
- 4 1 5 3 2 (tukar 5 dan 3) 4 1 3 5 2
- 4 1 3 5 2 (tukar 5 dan 2) 4 1 3 2 5
- 4 1 3 2 5 (tukar 4 dan 1) 1 4 3 2 5
- 1 4 3 2 5 (tukar 4 dan 3) 1 3 4 2 5
- 1 3 4 2 5 (tukar 4 dan 2) 1 3 2 4 5
- 1 3 2 4 5 (cocok)
- 1 3 2 4 5 (cocok)
- 1 3 2 4 5 (tukar 3 dan 2) 1 2 3 4 5
- 1 2 3 4 5 (cocok)
- 1 2 3 4 5 (cocok)
- 1 2 3 4 5 (cocok)
- 1 2 3 4 5 (cocok)
- 1 2 3 4 5 (cocok)
- 1 2 3 4 5 (cocok)
Berikut adalah implementasi dari Algoritma Bubble Sort dengan memakai prosedur. Parameter data berjenis referensi ke tipe data array of string:
procedure Bubble(var Arr: array of string);
var I: integer;
Ada_Tukar: boolean;
begin
repeat
Ada_Tukar:= false;
for I:= Low(Arr) to High(Arr)-1 do begin
if Arr[I] > Arr[I+1] then begin
Tukar(Arr[I], Arr[I+1]);
Ada_Tukar:= true;
end;
end;
until Ada_Tukar = false;
end;
SUMBER : http://id.wikibooks.org/wiki/Ayo_Membuat_Program_Pascal/Algoritma_Sorting_Dasar
SELECTION SORT
Selection Sort merupakan salah satu
algoritma pengurutan yang sederhana. Ide dasarnya adalah melakukan
beberapa kali pass untuk melakukan penyeleksian elemen struktur data.
Untuk sorting ascending (menaik), elemen yang paling kecil di antara
elemen-elemen yang belum urut, disimpan indeksnya, kemudian dilakukan
pertukaran nilai elemen dengan indeks yang disimpan tersebut dengan
elemen yang paling depan yang belum urut. Sebaliknya, untuk sorting
descending (menurun), elemen yang paling besar yang disimpan indeksnya
kemudian ditukar.
Selection Sort diakui karena
kesederhanaan algoritmanya dan performanya lebih bagus daripada
algoritma lain yang lebih rumit dalam situasi tertentu. Algoritma ini
bekerja sebagai berikut:
- Mencari nilai minimum (jika ascending) atau maksimum (jika descending) dalam sebuah list
- Menukarkan nilai ini dengan elemen pertama list
- Mengulangi langkah di atas untuk sisa list dengan dimulai pada posisi kedua
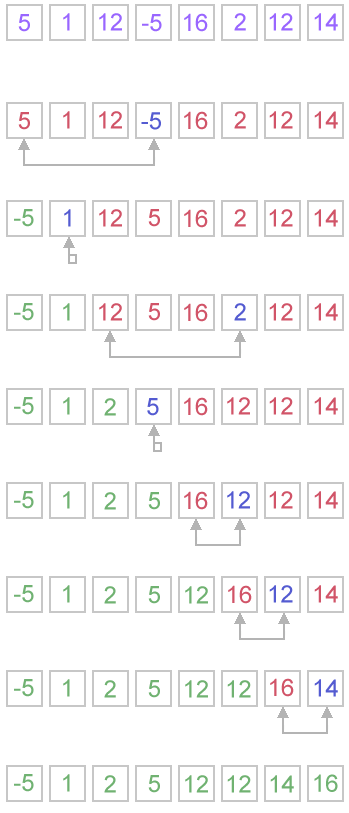
contoh simulasi algoritma selection sort sbb :
jika kita memiliki elemen array sbb : {5, 1, 12, -5, 16, 2, 12, 14}
Algoritma di dalam Selection Sort terdiri dari kalang bersarang. Dimana kalang tingkat pertama (disebut pass)
berlangsung
N-1 kali. Di dalam kalang kedua, dicari elemen dengan nilai terkecil.
Jika didapat, indeks yang didapat ditimpakan ke variabel min. Lalu
dilakukan proses penukaran. Begitu seterusnya untuk setiap Pass. Pass
sendiri makin berkurang hingga nilainya menjadi semakin kecil.
Berdasarkan operasi perbandingan elemennya.
implementasinya dalam bahasa pemrograman sbb :
/**
*
* @author Edi Zhou
*/
public class selectionSort {
int[] angka={5, 1, 12, -5, 16, 2, 12, 14};
public selectionSort()
{
tampilkanAngka();
urutkanAngka();
tampilkanAngka();
}
void tampilkanAngka()
{
System.out.println("\n--------------------------------");
for (int i=0;i<angka.length;i++)
{
System.out.print(angka[i]+" ");
}
}
void urutkanAngka()
{
int tampung;
for (int i=0;i<angka.length-1;i++)
{
int minindek=i;
for(int j=i+1;j<angka.length;j++)
{
if(angka[j]<angka[minindek])
minindek=j;
if(minindek!=i)
{
tampung=angka[i];
angka[i]=angka[minindek];
angka[minindek]=tampung;
}
}
//tampilkanAngka();
}
}
public static void main(String[] aksi)
{
selectionSort urut = new selectionSort();
}
}
*
* @author Edi Zhou
*/
public class selectionSort {
int[] angka={5, 1, 12, -5, 16, 2, 12, 14};
public selectionSort()
{
tampilkanAngka();
urutkanAngka();
tampilkanAngka();
}
void tampilkanAngka()
{
System.out.println("\n--------------------------------");
for (int i=0;i<angka.length;i++)
{
System.out.print(angka[i]+" ");
}
}
void urutkanAngka()
{
int tampung;
for (int i=0;i<angka.length-1;i++)
{
int minindek=i;
for(int j=i+1;j<angka.length;j++)
{
if(angka[j]<angka[minindek])
minindek=j;
if(minindek!=i)
{
tampung=angka[i];
angka[i]=angka[minindek];
angka[minindek]=tampung;
}
}
//tampilkanAngka();
}
}
public static void main(String[] aksi)
{
selectionSort urut = new selectionSort();
}
}
download source code disini
referensi :
- Munir, Rinaldi. 2003. Diktat Kuliah IF2153 Matematika Diskrit. Program Studi Teknik Informatika, Institut Teknologi Bandung.
- http://www.algolist.net/Algorithms/Sorting/Selection_sort
OUICK SORT
Pengenalan
Algoritma quick sort diperkenalkan pertama kali oleh C.A.R. Hoare pada tahun 1960, dan dimuat sebagai artikel di “Computer Journal 5” pada April 1962. Quick sort adalah algoritma sorting yang berdasarkan pembandingan dengan metoda divide-and-conqueror. Disebut Quick Sort, karena Algoritma quick sort mengurutkan dengan sangat cepat. Quick sort disebut juga dengan partition exchange sort, karena konsepnya membuat partisi-partisi, dan sort dilakukan per partisi.
(i) pilih x ϵ {a1, a2, …, an} sebagai elemen pivot.
(ii) pindai (scan) tabel dari kiri sampai ditemukan elemen ap ≥ x.
(iii) pindai tabel dari kanan sampai ditemukan elemen aq ≤ x
(iv) pertukarkan ap <-> aq
(v) ulangi (ii) dari posisi p + 1, dan (iii) dari posisi q – 1, sampai kedua pemindaian bertemu di tengah tabel.
Algoritma quick sort mengurutkan dengan sangat cepat, namun algoritma ini sangat komplex dan diproses secara rekursif. Sangat memungkinkan untuk menulis algoritma yang lebih cepat untuk beberapa kasus khusus, namun untuk kasus umum, sampai saat ini tidak ada yang lebih cepat dibandingkan algoritma quick sort.
Walaupun begitu algoritma quick sort tidak selalu merupakan pilihan yang terbaik. Seperti yang telah disebutkan sebelumnya, algoritma ini dilakukan secara rekursif yang berarti jika dilakukan untuk tabel yang berukuran sangat besar, walaupun cepat, dapat menghabiskan memori yang besar pula. Selain itu, algoritma ini adalah algoritma yang terlalu komplex untuk mengurutkan tabel yang berukuran kecil (hanya puluhan elemen misalnya). Selain itu algoritma quick sort mempunyai tingkat efisiensi yang buruk ketika dioperasikan pada tabel yang hampir terurut atau pada tabel yang terurut menurun.
Algoritma :
Pivot <- A[(i+j) div 2] { pivot = elemen tengah } p <- i q <- j repeat while a[p] <>= pivot }
while a[q] > pivot do
q <- q – 1 endwhile { Aq >= pivot }
if (p _ q) then
{ pertukarkan a[p] dengan a[q]}
temp <- a[p] a[p] <- a[q] a[q] <- temp { tentukan awal pemindaian berikutnya} p <- p+ 1 q <- q – 1 endif until p > q
Deklarasi :
k : integer;
Algoritma :
if (i
Partisi(a,i,j,k) { Ukuran (a) > 1}
QuickSort(a,i,k)
QuickSort(a,k+1, j)
Endif
Procedure Partisi (input/output: a : array[1..n] of integer, input i , j : integer, output q : integer)
{Membagi tabel a[i..j] menjadi subtabel a[i..q] dan a[q+1..j]. Keluaran upatabel a[i..q] dan subtabel a[q+1..j]. Sedemikian sehingga elemen tabel a[i..q] lebih kecil dari elemen tabel a[q+1..j]}
Deklarasi :
Pivot, temp : integer
Algoritma :
if (i
Partisi(a,i,j,k) { Ukuran (a) > 1}
QuickSort(a,i,k)
QuickSort(a,k+1, j)
Endif
Procedure Partisi (input/output: a : array[1..n] of integer, input i , j : integer, output q : integer)
{Membagi tabel a[i..j] menjadi subtabel a[i..q] dan a[q+1..j]. Keluaran upatabel a[i..q] dan subtabel a[q+1..j]. Sedemikian sehingga elemen tabel a[i..q] lebih kecil dari elemen tabel a[q+1..j]}
Deklarasi :
Pivot, temp : integer
Kompleksitas Algoritma Quick Sort
Kebutuhan waktu dari quicksort bergantung pada pembuatan partisi, seimbang atau tidak, yang bergantung juga pada elemen yang digunakan sebagai pivot. Dalam menghitung kompleksitas ini, perlu dilihat pula perhitungan recurrence, karena terdapat fungsi rekursif untuk penyelesaian sub-masalah.
Terdapat 3 jenis kompleksitas waktu dari quicksort:
1. Kasus terburuk (worst case), yaitu terjadi bila terbentuk partisi dengan komposisi sub-masalah antara n – 1 elemen dan 0 elemen. Dengan demikian pemanggilan fungsi secara rekursif dengan array berukuran 0 akan langsung kembali, T(0) = Θ(1), sehingga berlaku: T(n) = T(n – 1) + cn = O(n2).
2. Kasus terbaik (best case), yaitu terjadi bila terbentuk partisi dengan dengan komposisi seimbang, dengan ukuran masing-masing tidak lebih dari n/2. Sehingga didapat: T(n) = 2T(n/2) + cn = na + cn log n = O(n log n).
3. Kasus rata-rata (average case), yaitu terjadi dari perimbangan pivot antara terbaik dan terburuk, yang dalam prakteknya lebih mendekati kasus terbaik ketimbang terburuk. Sehingga didapat: Tavg(n) = O(n log n).
pivIndex = partition(x,first, last);
quicksort(x,first,(pivIndex-1));
quicksort(x,(pivIndex+1),last);
}
}
int partition(int y[], int f, int l) {
int up,down,temp;
int piv = y[f];
up = f;
down = l;
goto partLS;
do {
temp = y[up];
y[up] = y[down];
y[down] = temp;
partLS:
while (y[up] <= piv && up <> piv && down > f ) {
down–;
}
} while (down > up);
y[f] = y[down];
y[down] = piv;
return down;}
Program C++ Quicksort
#include
void tampilkan_larik(int data[], int n)
{
int i;
for (i=0;i
cout << x="data[a];" i="a;" j="c;"> x)
j=j-1;
while (data[i] < i="i+1;" tmp="data[i];" b="partisi(data," jum_data="8;">
SUMBER : sputniktotenkopf.blogspot.com/2010/03/quicksort.html
Tidak ada komentar:
Posting Komentar